Cardboard box optimization exercises

 Abstract

We study what integer dimensions of a rectangular piece of cardboard provide integer solutions to a standard optimization problem in introductory calculus.

Setup

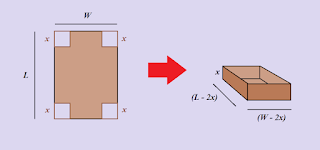
We have a rectangular piece of cardboard, of length 𝐿 and width 𝑊. Four equal-sized squares of sidelength 𝑥 are cut out of each corner, and the resulting flaps are folded up to produce a box. The quantity to be optimized is the volume 𝑉 of the resulting box.

Objective function & feasible domain

Once the squares are cut out, the dimensions of the base are 𝐿 - 2𝑥 and 𝑊 - 2𝑥, making our volume function

𝑉 = 𝑉(𝑥)

= 𝑥(𝐿 - 2𝑥)(𝑊 - 2𝑥)

= 4𝑥³ - 2𝑥²(𝐿 + 𝑊) + 𝑥𝐿𝑊.

The feasible domain for 𝑥 is

0 ≤ 𝑥 ≤ min(𝐿, 𝑊)/2.

Solution for 𝑥

We differentiate our objective function to find its stationary points:

d𝑉/d𝑥 = 12𝑥² - 4𝑥(𝐿 + 𝑊) + 𝐿𝑊,

and plugging directly into the Quadratic Formula, the stationary points occur at

𝑥 = [4(𝐿 + 𝑊) ± √{16(𝐿 + 𝑊)² - 48𝐿𝑊}]/24

𝑥 = [(𝐿 + 𝑊) ± √{(𝐿 + 𝑊)² - 3𝐿𝑊}]/6

𝑥 = [(𝐿 + 𝑊) ± √{𝐿² - 𝐿𝑊 + 𝑊²}]/6

Notice that the stationary points are homogeneous in 𝐿 and 𝑊, i.e. if we scale the box up by a factor λ, the stationary points

𝑥₋ = [(𝐿 + 𝑊) - √{𝐿² - 𝐿𝑊 + 𝑊²}]/6

𝑥₊ = [(𝐿 + 𝑊) + √{𝐿² - 𝐿𝑊 + 𝑊²}]/6

also scale by a factor λ. Therefore, if some particular values of 𝐿 and 𝑊 give rational but not integral values of 𝑥₋ and 𝑥₊, it's always possible to scale them so that 𝑥₋ and 𝑥₊ become whole numbers.

If L ≠ W, the stationary point x₊ is outside the feasible domain

Although the quadratic formula gives us two distinct stationary points 𝑥₋, 𝑥₊ when 𝐿 ≠ 𝑊, only one of them is feasible in the real-world context. Since √{𝐿² - 𝐿𝑊 + 𝑊²} > min(𝐿, 𝑊), it follows that

𝑥₊ = [(𝐿 + 𝑊) + √{𝐿² - 𝐿𝑊 + 𝑊²}]/6

> [3min(𝐿, 𝑊)]/6 = min(𝐿, 𝑊)/2

is never in the feasible domain, and can be omitted as a possible extremum.

Another way of seeing this: since our objective function 𝑉(𝑥) has zeroes at 𝑥 = 0, 𝑥 = 𝐿/2, and 𝑥 = 𝑊/2, then if 𝐿 ≠ 𝑊, by Rolle's theorem 𝑉(𝑥) must have a horizontal tangent in the open interval between 𝑥 = 𝐿/2 and 𝑥 = 𝑊/2. See Cardboard Box OptimizationVisualizer (desmos.com)

Getting "nice" rational answers

If we hope to get a rational answer for 𝑥₋, we need 𝐿² - 𝐿𝑊 + 𝑊² to be a perfect square. This is equivalent to specifying that we need 𝐿, 𝑊 to be two sides of a 60° triangle which has 3 integer sides, i.e. (𝐿, 𝑊, √{𝐿² - 𝐿𝑊 + 𝑊²}) form an Eisenstein triple. Wikipedia gives the following list of primitive Eisenstein triples for small values of 𝐿 and 𝑊:

Length, 𝐿	Width, 𝑊	√{𝐿² - 𝐿𝑊 + 𝑊²}
3	8	7
5	8	7
5	21	19
7	15	13
7	40	37
8	15	13
9	24	21

Plugging these values into the Quadratic Formula given above, we find the following values for 𝑥₋:

Length, 𝐿	Width, 𝑊	√{𝐿² - 𝐿𝑊 + 𝑊²}	𝑥₋
3	8	7	(3+8-7)/6 = 2/3
5	8	7	(5+8-7)/6 = 1
5	21	19	(5+21-19)/6 = 7/6
7	15	13	(7+15-13)/6 =3/2
7	40	37	(7+40-37)/6 = 5/3
8	15	13	(8+15-13)/6 = 5/3
9	24	21	(9+24-21)/6 =2

Wikipedia also gives the following recipe for generating other Eisenstein triples, which can be used to create other starting dimensions for the cardboard box problem with "nice" solutions for 𝑥₋.