It was relatively recently in my mathematical career that I learned that Brouwer-style intuitionism/constructivism had flowered into a valid and fascinating branch of mathematics in its own right. The popular histories I had read up to that point had presented Brouwer (despite his fixed-point theorem, and other studies on decidedly infinitary objects) as a dogmatic and essentialist finitist, who rejected every "completed infinity" as repugnant to the intuition.
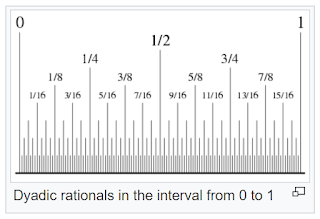
And insofar as an infinitely large object challenges--Brouwer would say defies--human imagination, it's difficult to argue, since our entire human existence is constrained within a fixed magnitude. Even the stellar distances and timescales which boggle the mind in relation to human scale, pale before the existence of an actual infinity, since every initial segment of ℕ is shorter by definition than the complementary tail segment, which is as long as ℕ itself, hence infinite. But an infinity which fits within a finite scale is not only conceivable, but visualizable. The infinite set of dyadic rationals in the range [0, 1], for instance, is directly perceptible at human scale:
Now I tried this argument out on a friend (with points on a banner rather than points on a segment) and he joshed me back that there were only finitely many points on the banner. If we want to move the goalposts to how many atoms or molecules the flag has, I'll concede that that's finite (if enormous, in the sextillion range, Area(Flag) × (conversion factor) × 6.022 × 10²³); but if we're talking about potential locations of an object on that same flag, then even the most dedicated doubter has to concede an actual infinity. So contra Brouwer, an actual infinity is not unintuitive. In fact, we may perceive it with our own eyes!
Yet an even more pertinent argument is available to the infinitist, who we might call a philosopher (of whatever flavor) who refuses to rule out the existence of actual infinities, whatever such a thing can mean. Once we have granted that a three, while an organizing description of a wide variety of real-world collections and measurements, has no actual real-world existence per se--that it is in fact an abstract concept/mathematical construct--what keeps us from regarding the square root of negative one, typically labeled in quasi-derogatory manner "the imaginary unit", on an equal epistemic status? And, once we are empowered to regard these objects as more or less equally valid, why should we not posit out of thin air an abstract concept which is countably infinite in magnitude, on the same epistemic status as the others? Even if such an object weren't capable of physically existing in the concrete universe--why should we deny ourselves its use as a conceptual tool to speed up and intuitify our proofs?
Does that mean the Brouwerian, both-hands-tied-behind-our-back, finitist method of math is useless? Not at all! On the contrary, versions of constructive math may have much to tell us about which mathematically conceivable goals are effectively computable. Additionally, such classic arguments as Euclid's proof of the infinitude of primes and Cantor's diagonal argument (both, as it so happens, regarding the relative infinitude of a particular mathematical object) are, or can be, made constructive. More generally, intuitionistic math has applications to computer programming, where constructiveness is built into the architecture.
Another active area of research is reverse mathematics--figuring out how much of math is left over without certain non-constructive principles. You could compare it to speedrunning a video game, or completing it at the lowest level possible, or avoiding the A-button as much as possible. Or in literature, an Oulipo-style project such as writing a novel with no 'e' - very good analogy because we are testing the limits of math's expressive power with/without certain foundational assumptions.

Comments
Post a Comment